Die Ostertage sind eine schöne Gelegenheit, um sich mit Ostereiern der ganz besonderen Art zu beschäftigen. „Erbrütet“ wurden sie vom Jülicher Quantenforscher Dr. Robert Zeier, gemeinsam mit Kollegen in Oxford und München. Die bunten Kugeln zeigen Zustände, die man sich eigentlich nur sehr schwer bildlich vorstellen kann. Sie entstehen, wenn sehr viele Quantenbits, auch Qubits genannt, miteinander verschränkt werden.
Mit diesem Tweet hatte das PASQUanS-Projekt aus dem europäischen Quanten-Flaggschiff-Projekt die Arbeit im Januar vorgestellt. „Uns ging es darum, das Verständnis zu verbessern und ein einfaches Werkzeug zu entwickeln, mit dem man sich schnell einen Überblick verschaffen kann. Zum Beispiel wenn man wissen möchte, in welchem Zustand sich ein Quantenexperiment gerade befindet“, erklärt Dr. Robert Zeier.

Der Informatiker Dr. Robert Zeier beschäftigt sich schon seit über 20 Jahren mit Quantendingen und stieß 2019 nach Stationen in Karlsruhe, Harvard und der TU München zur Gruppe von Professor Tommaso Calarco am Forschungszentrum Jülich.
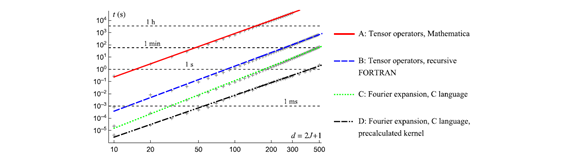
Das Besondere an der neuen Methode, die er nun mit seinen Kollegen in der Fachzeitschrift Physical Review A vorgestellt hat, ist die Geschwindigkeit.
Copyright: Koczor, Zeier, Glaser, Phys. Rev. A, DOI: https://doi.org/10.1103/PhysRevA.102.062421 (CC BY 4.0)
Das Verfahren ist tausendmal schneller als gängige Algorithmen. „Wir wollten eine Methode, die einfach ist und die im Alltag gut funktioniert. Für eine solche Visualisierung mit mehreren hundert Qubits hat man mit einem modernen PC bisher über eine Stunde gebraucht, das macht man nicht mal so eben nebenbei“, erläutert Zeier. „Mit unseren Ansatz schafft man es dagegen teilweise unterhalb einer Sekunde. Das ist in der Praxis ein Riesenvorteil!“
Copyright: Koczor, Zeier, Glaser, Phys. Rev. A, DOI: https://doi.org/10.1103/PhysRevA.102.062421 (CC BY 4.0)
Was zeigen die Kugeln?
Stellt sich natürlich die Frage, was genau hier eigentlich zu sehen ist. Klar ist, dass es für die „Quanten-Ostereier“ in der realen Welt keine bildliche Entsprechung gibt. Denn Ort und Energie der Quantenzustände, um dies hier geht, sind gar nicht exakt festgelegt. Das besagt die sogenannte Heisenbergsche Unschärferelation.
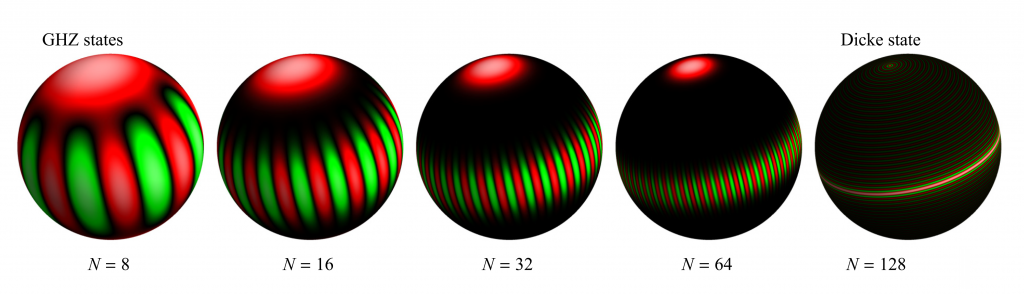
Die Farben auf den „Quanten-Ostereiern“ kennzeichnen vielmehr das Ergebnis der sogenannten Wigner-Funktion. Der ausgewählte GHZ-Zustand, dazu später mehr, spielt etwa für Quantencomputer und grundsätzliche physikalische Überlegungen eine wichtige Rolle.
Die Gundlagen
Quantenbits sind die Grundeinheiten, mit denen ein Quantencomputer rechnet. Ein klassisches Bit kann üblicherweise nur 0 oder 1 sein. Ein Qubit kann dagegen gleichzeitig verschiedene Werte annehmen. Physiker sprechen hier von „Überlagerung“. Erst wenn man nachmisst, entscheidet sich, ob das Qubit eine 0 ist oder eine 1.

Forschungszentrum Jülich / Annette Stettien
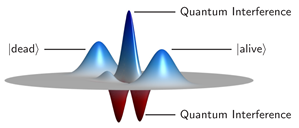
Das Grundprinzip beschreibt Schrödingers Gedankenexperiment mit der Katze. Während die Katze in der makroskopischen Welt nur tot oder lebendig sein kann, gibt es in der Quantenwelt auch Überlagerungszustände, in denen sie beides gleichzeitig ist.
Das Prinzip der Überlagerung erlaubt also, dass die Qubits gleichzeitig verschiedene Zustände annehmen können. Ein Quantencomputer kann so in einem Schritt sehr viele Rechenoperationen auf einmal ausführen. Dieser Quantenparallelismus ist auch ein Grund dafür, dass Quantencomputer manche Probleme im Vergleich zu bekannten Methoden auf klassischen Rechnern viel schneller lösen können.
Ein weiteres wichtiges Merkmal von Qubits: sie lassen sich miteinander verschränken. Misst man verschränkte Qubits, dann zeigt sich, dass sie auf geheimnisvolle Art miteinander verbunden sind: Wenn das eine Qubit eine 1 ist, so erhält man für das andere immer den gleichen – oder immer den umgekehrten – Wert.
Die Verschränkung von Qubits ist auch eine der Aufgaben, mit denen sich Forschende am Jülicher Peter Grünberg Institut für Quantum Control, an dem Robert Zeier tätig ist, beschäftigen. 2019 hatten sie zusammen mit Partnern von mehreren amerikanischen Universitäten 20 Quantenbits miteinander verschränkt und damit einen neuen Rekord aufgestellt.
Die Wigner-Funktion
Quantencomputer rechnen mit potenziell verschränkten Überlagerungszuständen, genau darin liegt ihr Potenzial. In der Forschung will man diese Zustände erfassen, etwa um das Ergebnis von Quantenexperimenten nachzuvollziehen, oder um die Funktion von Quantenschaltkreisen zu überprüfen. Dabei tun sich schnell Schwierigkeiten auf.
„Man kann Quantenzustände auch mithilfe sogenannter Dichtematrizen beschreiben. Wenn diese Matrix aber 500 mal 500 Einträge hat, dann wird das sehr unübersichtlich“, erklärt Robert Zeier. „Experimentatoren und Theoretiker wollen daher häufig gerne die Wigner-Funktion sehen.“
Copyright: Rundle et al., Phys. Rev. A, DOI: https://doi.org/10.1103/PhysRevA.96.022117 (CC BY 3.0)
Die Funktion geht auf den Nobelpreisträger Eugene Wigner zurück und macht es möglich, die verschiedenen Überlagerungszustände auf einen Schlag sichtbar zu machen. Die Wigner-Verteilung gibt für jeden möglichen Zustand eines Systems eine „Quasi-Wahrscheinlichkeit“ an: „Quasi“, weil die Wigner-Funktion auch negative Werte annehmen kann. Klassische Wahrscheinlichkeiten sind dagegen nie niedriger als Null.
Verschränkte Zustände
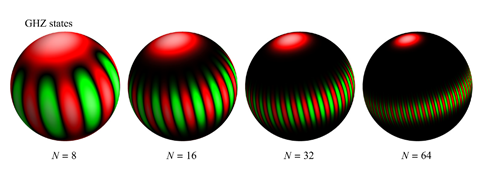
Robert Zeier und seine Kollegen haben die Wigner-Funktion allerdings nicht wie oben auf der z-Achse über einer flachen Ebene aufgetragen. Stattdessen haben sie die Ergebnisse auf eine Kugeloberfläche projiziert. Die Quasi-Wahrscheinlichkeiten haben sie dabei über eine Farbkodierung kenntlich gemacht: rote Flächen markieren positive, grüne negative Werte.
„Die Kugeloberfläche ist begrenzt, anders als die flache Ebene, die ja im Prinzip bis ins Unendliche geht. Diese begrenzte Fläche und deren Rotationssymmetrie passt sehr gut zu den Quantensystemen und Zuständen, die uns interessieren und die ebenfalls endlich sind“, erklärt Robert Zeier.
Copyright: Koczor, Zeier, Glaser, Phys. Rev. A, DOI: https://doi.org/10.1103/PhysRevA.102.062421 (CC BY 4.0)
Der nach den Physikern Greenberger, Horne und Zeilinger benannte GHZ-Zustand bezeichnet ein System mit mehreren Qubits, die maximal miteinander verschränkt sind. Das bedeutet: Bei einer Messung befinden sich alle Qubits im gleichen Zustand. Man erhält also entweder eine 000 oder eine 111.
Ursprünglich bezeichnete der GHZ-Zustand ein Quantensystem mit drei Teilchen. Mittlerweile fallen aber auch Systeme mit deutlich mehr Qubits unter den Begriff, wie in den Visualisierungen von Robert Zeier und seinen Kollegen. Die Zustände 0000… und 1111… liegen darin an den beiden Polen, während sich die verschränkten Zustände als grün-rot gestreiftes Band um die Kugel ziehen.
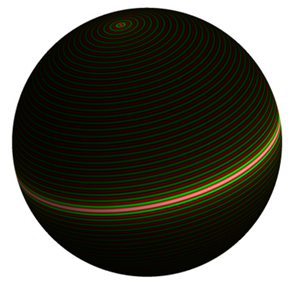
Dicke-Zustand mit 128 Qubits
Copyright: Koczor, Zeier, Glaser, Phys. Rev. A, DOI: https://doi.org/10.1103/PhysRevA.102.062421 (CC BY 4.0)
Qubits im Dicke-Zustand – benannt nach dem Physiker Robert Dicke – sind ebenfalls miteinander verschränkt, wenn auch nicht ganz so stark wie im GHZ-Zustand. Dicke-Zustände werden in der Forschung oftmals als Modellsystem eingesetzt und lassen sich im Labor mittlerweile routinemäßig herstellen. Charakteristisch für Dicke-Zustände ist, dass die Qubits nach einer Messung ein bestimmtes Verhältnis von Nullen und Einsen aufweisen, also zum Beispiel 0011, 0101, 1100, 1010, während sich im verschränkten Zustand alle diese Permutationen überlagern.

No Comments
Be the first to start a conversation