Elektrische Dipolmomente sind im Alltag eigentlich nichts besonders. Sie entstehen, wenn die Schwerpunkte von positiver und negativer Ladung in einem Objekt gegeneinander verschoben sind. Ohne sein Dipolmoment hätte z.B. das Wasser, auf dem unser aller Leben beruht, andere physikalische Eigenschaften. Auf der Ebene von Protonen und Neutronen sieht das aber ganz aus.
Warum ist das so? Protonen und Neutronen (als Beispiel) haben eine definierte Parität, d.h. ihre quantenmechanische Wellenfunktion (eine abstrakte mathematische Beschreibung, die ein Objekt komplett beschreibt) bleibt bei einer Spiegelung bis auf das Vorzeichen gleich. Hier kann man sich als Hilfe eine Wasserwelle vorstellen, die so aussieht, dass bei einer Spiegelung Wellenberge zu Wellentäler werden können und umgekehrt. Ändert sich das Vorzeichen nicht (d.h. Wellenberge bleiben Wellenberge und Täler bleiben Täler), spricht man von positiver Parität, ansonsten von negativer Parität. (Sehr) grob gesagt, sind das Objekte, die an sich schon symmetrisch sind und deren innere Struktur – wenn es sich nicht um ein Elementarteilchen ohne eine solche handelt – keine definierte Ausrichtung hat. Passende Vergleiche im Alltag sind hier nicht wirklich möglich, anführen könnte man die homogene Kugel, die keine Änderung zeigt bzw. einen Vektorpfeil, der sich durch Spiegelung umkehrt und durch Drehung wieder zurückgebracht werden kann. Ein gespiegelter Mensch hat keine definierte Parität.
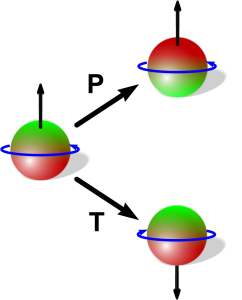
Schauen wir uns einmal ein Neutron an (links). Dieses hat einen Eigendrehimpuls (Spin, schwarz, siehe letzten Beitrag), dessen Drehrichtung auch noch einmal in Blau dargestellt ist. Es hat auch ein magnetisches Moment, welches klassisch durch eine rotierende Ladungsverteilung erzeugt werden würde. Quantenmechanisch ist dieses Bild zwar nicht korrekt, aber das magnetische Moment ist auch hier parallel zum Spinvektor und man kann sich zur Illustration durchaus auch mal einen imaginären Kreisstrom vorstellen, der durch den blauen Pfeil beschrieben wird.
Was passiert bei einer Spiegelung (P)? Wie schon in einem früheren Beitrag angemerkt, ändert sich die Rotationsrichtung bei einer Punktspiegelung nicht: Spin und magnetisches Moment bleiben gleich. Bis hierher ist also alles in Ordnung. Ein elektrisches Dipolmoment ändert hier aber so einiges. Da das Neutron – wieder mal klassisch und nicht quantenmechanisch gesehen – durch den Eigendrehimpuls rotationssymmetrisch sein muss, kann eine Ladungsverschiebung nur entlang des Spins stattfinden. Im Bild wird das durch rote und grüne Bereiche dargestellt, die für eine positive bzw. negative Ladung stehen. Wenn ich diese spiegele, werden die beiden Bereiche vertauscht. Im Ergebnis habe ich also ein Objekt, dass sich vom Ausgangszustand unterscheidet: die Parität wird verletzt.
Ähnlich verhält es sich bei der Zeitumkehr (T). Hier bleiben die Ladungen an Ort und Stelle, aber der Spin (die Rotation) dreht sich um, wenn ich die Zeitrichtung ändere. Ohne elektrisches Dipolmoment würde sich der Spin zwar auch umkehren, aber das Objekt als Ganzes würde seine Eigenschaften nicht ändern. Aus dem bereits angesprochenen CPT Theorem folgt nun noch, dass auch CP verletzt sein muss, also genau das, von dem wir bisher „zu wenig“ haben.
Wie groß sind nun die elektrischen Dipolmomente (EDMs), von denen wir hier reden? Ein EDM d misst man über die Stärke der Ladungen Q, die verschoben wurden, und deren Abstand R: d = Q x R. In der Teilchenphysik ist die Elementarladung e eine gute Bezugsgröße und so wird als Einheit meist e cm, also Elementarladung mal Abstand in Zentimetern gewählt. Ein Proton oder Neutron hat einen Radius von etwa 10-13 cm. Nimmt man an, die Ladung hätten sich soweit wie möglich separiert, hätte man also ein EDM von 2 x 10-13 e cm. Um diese Skalen zu verdeutlichen wird meist der Kölner Dom bemüht: wäre das Wasserstoffatom so groß wie der Dom, hätte das Proton als Atomkern gerade einmal Kir(s)chkerngröße – auf dieser Skala wäre der Abstand Erde-Mond allerdings gerade einmal das Doppelte der Dicke eines menschlichen Haares … Wirklich anschaulich ist das also auch nicht.
Aber an dieser Stelle ist nicht Schluss. Da ein solches EDM nur mit CP-Verletzung erklärt werden kann und im Standardmodell der Teilchenphysik CP-Verletzung nur als relativ kleiner Effekt in der schwachen Wechselwirkung bekannt ist, sind die Vorhersagen des Standardmodells natürlich noch viel kleiner: sie liegen im Bereich von weniger als 10-30 e cm – eine Zahl, die man nun wirklich nicht mehr beschreiben kann. Eines ist aber klar: die CP-Verletzung im Standardmodell reicht nicht aus, um den Materieüberschuss im Universum zu erklären. Alle diskutierten Erweiterungen des Standardmodells liefern daher auch weitere Quellen zur CP-Verletzung und sagen größere elektrische Dipolmomente voraus. Damit sind solche Präzisionsmessungen auch neben der direkten Suche nach neuen, sogenannten supersymmetrischen Teilchen (wie sie am LHC oder einer geplanten, noch größeren Maschine durchgeführt wird) ein zweites Standbein, wenn es um die Überprüfung dieser Theorien geht.
Die Suche nach EDMs ist nicht neu. Bereits 1951 wurde von Smith, Purcell und Ramsay eine obere Grenze von 5 x 10-20 e cm für das Neutron gemessen. Dieser Wert wurde bis heute in vielen verschiedenen Experimenten bis auf 2.9 x 10−26 e cm verbessert (Baker et al.). Auch in anderen Systemen (Atome, Moleküle) wurde danach gesucht, wobei alle diese Messungen eines gemeinsam haben: es handelt sich um neutrale Systeme. Auch die aktuellen Grenzen für Protonen oder Elektronen wurden auf dieser Basis mit Hilfe von theoretischen Modellen indirekt bestimmt – mit entsprechenden systematischen Unsicherheiten. Direkte Messungen gibt es hier keine.
Der Grund dafür ist relativ einfach: um elektrische Dipolmomente zu messen muss man starke äußere elektrische Felder anlegen. Geladene Teilchen würden durch diese beschleunigt und verloren gehen. Allerdings gibt es sehr gute Gründe, auch das EDM von geladenen Teilchen wie Protonen oder Deuteronen direkt zu messen. Sollte z.B. ein EDM für das Neutron gefunden werden, stellt sich immer noch die Frage nach dem zugrunde liegenden Mechanismus. Hier bieten die Theorien jenseits des Standardmodells einige Optionen an. Nur durch Messungen der EDMs verschiedener Teilchen können hier entsprechenden Rückschlüsse gezogen werden. Auch haben Experimente mit Protonen das Potential zu niderigeren Grenzen vorzustoßen, da Messungen mit Neutronen immer mit deren Lebensdauer und deren Erzeugung zu kämpfen haben.
Im Gegensatz zu Neutronen kann man Protonen oder Deuteronen also nicht einfach in ein Gefäß sperren und ein elektrisches Feld anlegen. Was tut man stattdessen? Die Beschleunigung in einem elektrischen Feld erinnert sofort an einen Teilchenbeschleuniger. Genau da setzen wird an: die geladenen Teilchen werden durch die Felder, mit denen das elektrische Dipolmoment gemessen werden soll, nicht nur beschleunigt, sondern auch auf einer Kreisbahn in einem Speicherring gehalten. Und hier kommen wir nun endlich zum Experiment, zu COSY und zu den technischen Herausforderungen, die auf uns warten bzw. die in den letzten Jahren schon angegangen wurden.

One Response to “Klein, kleiner, am kleinsten, EDM”