Wie „dressiert“ man eigentlich Deuteronen? – Teil 2

In diesem Artikel möchte ich ein neues „Glückspiel“ entwickeln – und zwar eine Mischung aus Roulette und Münzwurf. Das mag auf den ersten Blick nicht viel mit sich drehenden und präzidierenden Deuteronen zu tun haben, wird aber eine unserer experimentellen Fragestellungen relativ gut beschreiben.

36 gezinkte Münzen

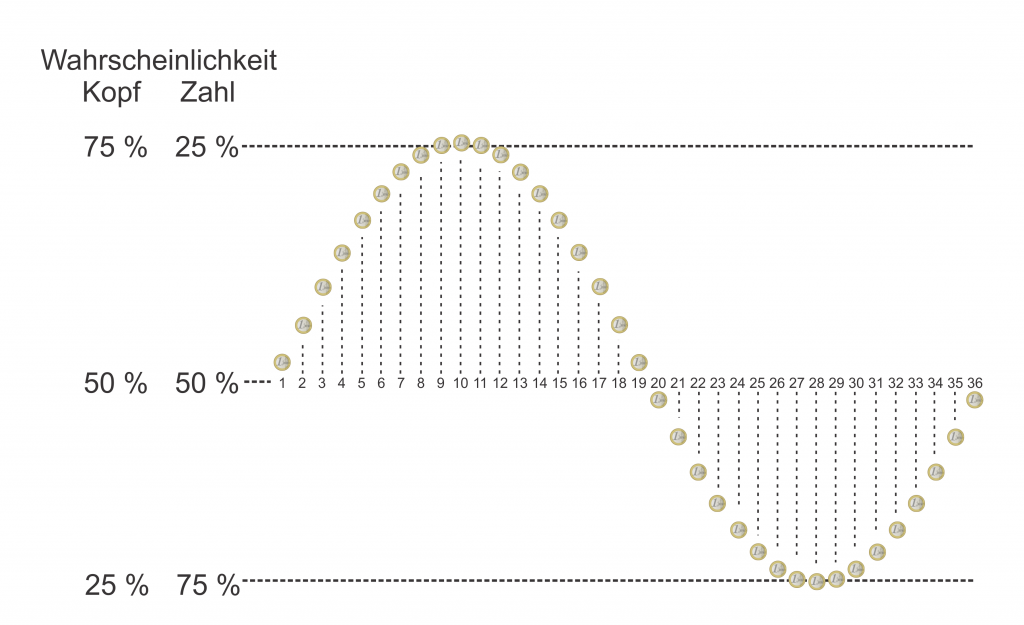
Stellen wir uns einmal vor, wir haben 36 Münzen. Normalerweise sollte bei jedem Wurf und mit jeder Münze die Wahrscheinlichkeit Kopf oder Zahl zu erhalten 50% betragen. Nicht so bei unseren Münzen. Diese haben die im unteren Diagramm aufgetragene Wahrscheinlichkeiten:

Wahrscheinlichkeitsverteilung der gezinkten Münzen (Bild: VH)

Alle Münzen sehen gleich aus. Um herauszufinden, welche Münze wie gezinkt ist, muss man die Münze werfen. Ein Wurf alleine reicht nicht – nur wenn ich sehr oft werfe, nähert sich mein Meßwert (z.B. Würfe mit Kopf geteilt durch die Gesamtzahl) der tatsächlichen Wahrscheinlichkeit an.

Hier findet sich die erste Analogie: Wenn ich den Polarisationsgrad eines Ensembles messen möchte, vergleiche ich, wie viele Teilchen bei einer Streuung zur einen und wie viele zur anderen Seite fliegen (siehe hier). Ist das Ensemble unpolarisiert, ergibt sich eine Wahrscheinlichkeit von 50:50. Je nach Polarisation verschiebt sich diese in die eine oder andere Richtung.

So weit, so gut: Bei einer einzelnen Münze kann ich beliebig oft werfen und die Genauigkeit meines Ergebnisses hängt nur von meinem Fleiß ab. Was aber, wenn ich nicht immer dieselbe Münze bekomme?

Münzen auf dem Rouletterad

Dazu baue ich mir ein Rouletterad mit 36 „Feldern“. Jedes dieser Felder besteht aus einem Magazin zur Aufnahme einer „großen Menge“ Münzen. Dazu besorge ich von jeder Sorte gezinkter Münzen einen entsprechenden Vorrat und befülle die Magazine entsprechend ihrer Nummerierung. An einer Stelle am Tisch befindet sich ein Auslösemechanismus, der auf Knopfdruck einen Münzwurf aus dem Magazin bewirkt, das gerade vorbeikommt.

Vor-Experiment 1:

Wir drehen das Rad mit einer Frequenz von einer Umdrehung pro Sekunde. Auch den Auslöser betätigen wir kontinuierlich im Abstand von einer Sekunde. Das führt dazu, dass immer das gleiche Feld ausgelöst wird. Welches das ist, bestimmt die Anfangsbedingung. Mit den Münzwürfen bestimmen wir so die Eigenschaft einer einzigen Münze.

Vor-Experiment 2:

Wir drehen das Rad weiterhin mit einer Frequenz von einer Umdrehung pro Sekunde. Der Auslöser läuft aber nun mit einer beliebigen anderen Frequenz. Nun wird der Münzwurf nicht immer für das gleiche Feld ausgelöst. Wenn wir aber die Frequenz des Auslösers kennen und auch welches Feld sich am Anfang neben dem Auslöser befand, können wir ausrechnen, für welches Feld der Münzwurf jeweils ausgelöst wird. Wir können uns dann eine Tabelle von 1 bis 36 machen und die Ergebnisse für jedes Feld notieren. Insgesamt sollten wir dann die Wahrscheinlichkeitsverteilung in der obigen Abbildung messen.

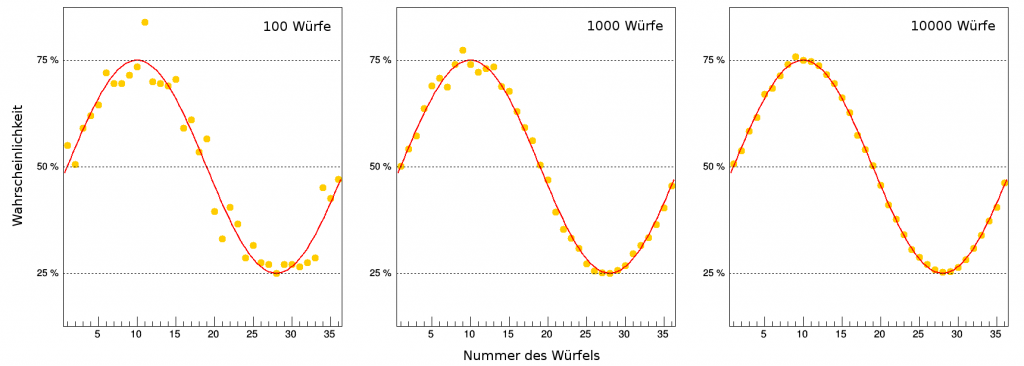
Wie genau wir diese Abbildung reproduzieren können, hängt von der Zahl der Würfe ab. Von links nach rechts zeigen die Bilder unten den Anteil an Kopfwürfen bei 100, 1000 bzw. 10000 Würfe pro Münze.

Auswirkungen der Zahl der Würfe (Bild: VH)

Vor-Experiment 3:

Das ganze funktioniert natürlich nur, wenn die Frequenz des Auslösers und des Rades in keinem einfachen Verhältnis zueinander stehen. Ansonsten entsteht eine feste Folge, die meist auch nicht alle Felder beinhaltet. Um das zu umgehen, lassen wir den Auslöser nicht mehr mit einer festen Frequenz laufen, sondern schließen ihn an einen Zufallsgenerator an (schließlich sind die physikalischen Prozesse, die wir beobachten, auch von statistischer Natur). Zusätzlich messen wir nun jeweils den Zeitpunkt, zu dem er einen Münzwurf auslöst. Da wir die Frequenz des Rouletterades kennen, können wir auch hier wieder ausrechnen, wann welches Feld am Auslöser vorbei kommt. Im Endeffekt bekommen wir so die gleichen Ergebnisse wie vorher.

Haupt-Experiment:

Bisher sind wir davon ausgegangen, dass wir die Frequenz des Rouletterades kennen. Was aber, wenn nicht? Können wir diese Frequenz eventuell mit dieser Methode sogar messen? Wie wir später sehen werden, ist das genau die Frage, mit der wir uns auch in unseren Experimenten an COSY beschäftigt haben und die wir schließlich mit „ja“ beantworten konnten.

Wäre die Frequenz der Einzelmessungen (also die des Auslösers) sehr viel größer als die des Rades, wäre der Auslöser für mehrere Würfe hintereinander am gleichen Feld. So könnte man immer eine bestimmte Zahl von Messwerten zusammenfassen und die Kurve zumindest mit kleiner Statistik „abtasten“. Mit Hilfe einer mathematischen Methode (Ausgleichsrechnung) könnte dann die rote Schwingungskurve bestmöglich eingepasst werden um so die Rotationsdauer oder die Frequenz zu erhalten.

Hier geht es um den umgekehrten Fall: die Frequenz des Rouletterades ist wesentlich größer als die Abtastrate durch den Auslöser. Zwischen den einzelnen Würfen dreht sich das Rad mehrere Male. Da uns ein einzelner Wurf keine Aussage über die Häufigkeit von Kopf oder Zahl liefert, sondern nur die binäre Information Kopf oder Zahl, kann ich keine Rückschlüsse auf das Feld ziehen, auf dem die Münze lag. Was ich bekomme sind Wertepaare aus dem Zeitpunkt des Wurfes und dem Ergebnis Kopf oder Zahl.

Wie das geht und warum das überhaupt eine der zentralen Fragen waren, mit denen wir gestartet sind, werde ich dann beim nächsten Mal erläutern.