Wie „dressiert“ man eigentlich Deuteronen? – Teil 1

Oder auch: Wie hütet man eine Herde Deuteronen? In jedem Messzyklus arbeiten wir mit einigen Milliarden Deuteronen, die im Beschleuniger kreisen – also etwa so viele wie es Menschen auf der Erde gibt.  Für unsere Messungen ist es notwendig, dass sich möglichst viele diese Deuteronen über den gesamten Messzyklus genau gleich verhalten. Für die Präzession des Spins bedeutet das in unserem Fall, dass die Deuteronen völlig synchron etwa 100 Million Pirouetten drehen müssen.

Warum ist das notwendig? Wie ich hier erklärt habe, ist die Messung der Spinrichtung (oder genauer der Polarisation eines Ensembles) ein statistischer Prozess: Ich muss viele Einzelmessungen ausführen, um dann über den Mittelwert bzw. die Verteilung der Ergebnisse eine Aussage treffen zu können. Nun ist aber jedes Deuteron, dass ich für eine Messung verwende, „verbraucht“. Es ist aus dem Strahl entfernt (mit Hilfe eines Targets herausgestreut) und steht nicht weiter zur Verfügung. Ich muss mich also darauf verlassen, dass alle Deuteronen, die ich verwende, vor der Messung die gleiche Spinausrichtung haben – ansonsten funktioniert die Messung nicht und ich bekommen eine „Null“ für die Polarisation.

Das ist der eine Grund. Der andere ist, dass ich aus den „verbrauchten“ Deuteronen auf alle anderen Deuteronen schließen möchte. Die Idee der EDM Messung besteht ja darin, eine (kleine) Änderung der Spinrichtung über den Messzyklus hinweg zu messen. Dazu muss ich annehmen, dass eine Messung am Anfang (und während) des Zyklus auch repräsentativ für die Deuteronen ist, die im Strahl verbleiben und die ich später im Zyklus für Messungen verwenden will.

In unsere Sprache übersetzt bedeutet das, dass die Spins der einzelnen Deuteronen kohärent mit der gleichen Frequenz präzedieren sollten – und die Zeit über die sie das tun, nennen wir Spinkohärenzzeit. Natürlich verhalten sich hierbei nicht alle Deuteronen absolut identisch, sondern die Spinausrichtung wird mit der Zeit immer weiter auseinanderlaufen und der Polarisationsgrad des Ensembles wird nicht schlagartig, sondern kontinuierlich abnehmen. Eine gängige Definition der Spinkohärenzzeit ist z.B. die Zeit, in der die Polarisation auf die Hälfte abgefallen ist.

Dabei gibt es experimentell folgende Dinge (unter anderem) zu beachten:

1. Das Deuteronenensemble muss mit einem möglichst hohen Polarisationsgrad in den COSY-Ring injiziert werden.
2. Die Präzessionsfrequenz soll genau vermessen werden.
3. Die Spinkohärenzzeit soll maximiert werden.
4. Für kommende Experimente: Die Präzession der Deuteronen soll sogar gesteuert werden.

Für die Punkte 2 bis 4 sind neue Experimentiermethoden notwendig gewesen, die wir in den letzten 3 Jahren entwickelt und mittlerweile auch alle in Physics Review Letters veröffentlich haben (2015, 2016, 2017).  In diesem Artikel möchte ich noch den allgemein Experimentaufbau erklären und dann für die nächsten Punkte jeweils einen eigenen Artikel verwenden.

Messprinzip (Bild: VH / Forschungszentrum Jülich)

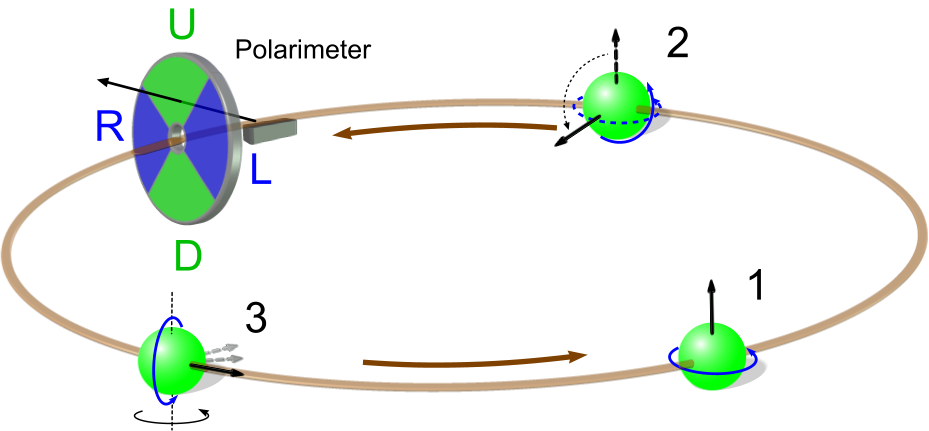
Das Bild oben zeigt das generelle Messprinzip. Zunächst werden die Deuteron mit Spinausrichtung nach oben in den Ring injiziert. In einem Speicherring wie COSY ist die vertikale Achse die sogenannte invariante Spinachse. Um diese Achse präzediert der Spin, d.h. die Spinkomponente parallel zu dieser Achse ist stabil – unabhängig von der Präzessionsfrequenz um diese Achse. Die Teilchenensembles, die so im Speicherring landen, haben bei COSY typischerweise eine Polarisation zwischen 50% und 80%. Lässt man einen solchen Teilchenstrahl nun ungestört umlaufen, können sowohl der Strahl als die Polarisation für mehrere Stunden aufrecht erhalten werden. Den Polarisationsgrad kann man mit Hilfe eines Polarimeters messen, indem man die Asymmetrie der Zählraten links und rechts des Strahl misst (wie hier beschrieben).

Allerdings interessieren wir uns ja für die Präzession um die vertikale Achse und die Frage, wie lange unter diesen Bedingungen der Polarisationsgrad erhalten bleiben kann. Dazu nutzen wir in Schritt 2 einen sogenannten RF Solenoidmagneten. Dieser besteht im wesentlich aus einer Spule, deren Mittelachse auf der Teilchenbahn liegt und durch die ein Wechselstrom fließt (RF = radio frequency). Die Frequenz wird so eingestellt, dass eine Resonanzbedingung aus Umlauffrequenz (in unserem Fall etwa 750 kHz) und der Präzessionsfrequenz (120 kHz) entsteht. In diesem Fall beginnt der Spin langsam senkrecht zur Flugrichtung zu präzedieren: Immer wenn die Teilchen durch den Solenoiden fliegen, wird der Spin ein Stück weiter gedreht. Eventuell werde ich das später in einem eigenen Artikel nochmal genauer erklären.

Sobald die Spinrichtung in der horizontale Ebene liegt, schalten wir den Solenoiden aus. Typischerweise dauert das – je nach Stärke des Stromes – einige Sekunden. Die Seitwärtsrichtung in der horizontalen Ebene zum Zeitpunkt des Abschaltens stellt auch die Anfangsbedingung für unsere Messungen dar. Hier sollte der Polarisationsgrad immer noch dem entsprechen, mit dem das Teilchenensemble eingeschossen wurde.

Nun beginnt der Spin der einzelnen Teilchen zu präzedieren – und zwar bei unseren Teilchenenergien mit etwa 120 kHz. Die Messung des Polarisationsgrads erfolgt im Prinzip genau wie vorher. Da nun aber die Spinachse gedreht ist, sind nun die Detektoren oberhalb und unterhalb (Up, Down) maßgeblich. Dazu kommt aber noch die Schwierigkeit, dass man mit diesen Zählern eigentlich nur die Polarisation entlang der horizontalen Achse senkrecht zur Strahlrichtung messen kann. Da die Spins aber präzedieren, oszilliert die Projektion der Spinrichtung auf diese Achse ebenfalls mit 120 kHz. Eine stabile Langzeitmessung wie für die vertikale Polarisation ist also nicht möglich. Der Lösung dieses Problems werde ich mich im nächsten Artikel widmen.