Was Fahrrad fahren mit der Messung von elektrischen Dipolmomenten zu tun hat

So ein Kreisel ist schon ein seltsames Ding. Wenn man seine Achse in eine bestimmte Richtung drehen will, wird sie nicht einfach folgen. Stattdessen wird der Kreisel mit seiner Achse zur Seite ausweichen. Das widerspricht zwar irgendwie unseren naiven Erwartungen, aber jeder Fahradfahrer nutzt genau dieses Prinzip intuitiv zum Kurvenfahren – und wir nutzen es zur Messung elektrischer Dipolmomente.

Präzession eines Kreisels (Bild: VH)

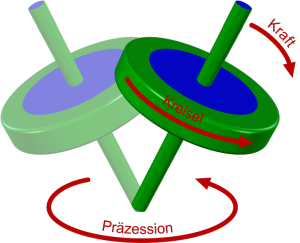
Normalerweise kann ich nicht einfach irgendwas schief in die Landschaft stellen und erwarten, dass es nicht umfällt. Sowas geht nur bei einem – sich natürlich auch drehendem – Kreisel. Stellt man diesen schräg, versucht die Schwerkraft diesen weiter nach unten zu drehen. Da ein Kreisel aber zur Seite ausweicht, beginnt er stattdessen eine zweite, überlagernde Drehbewegung um die senkrechte Achse herum auszuführen. Diese Drehbewegung nennt ein Physiker Präzession – aber keine Angst, ich werde jetzt keine trockene Beschreibung der Details mit Hilfe von Drehimpulsvektoren anfangen, für unsere Zwecke hier reicht das Prinzip.

Kurven fahren (Bild: VH)

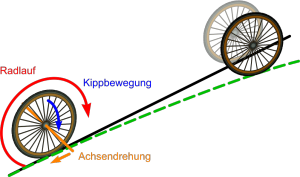
Wie schon oben angedeutet scheint das zwar unseren naiven Erwartungen zu widersprechen, im Alltag nutzen wir es aber trotzdem, nämlich beim Fahrad fahren. Das, was das Fahrad im normalen Fahren in die Kurve bringt ist die Schräglage: durch das Kippen des Rades dreht sich die Achse um die Vertikale und gibt dem Rad eine andere Richtung. Der Lenker dient eigentlich nur dazu, diese Schräglage einzuleiten und zu kontrollieren. (Und nebenbei, weil es auch eine Bewegung ist, die den meisten gar nicht bewusst ist: die Schräglage wird durch eine kurze Lenkbewegung in die entgegengesetzte Richtung eingeleitet – ohne diese würde das nicht funktionieren.) Damit verhält sich ein Fahrrad völlig anders als z.B. ein Auto oder ein Dreirad. Deswegen sind z.B. Stützräder auch eine ziemlich schlechte Methode Fahrrad fahren zu lernen.

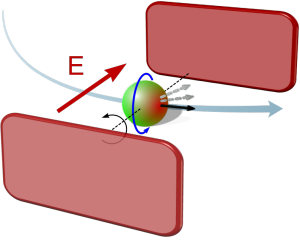
Präzession im elektrischen Feld aufgrund eines EDMs. Der mit E bezeichnete Pfeil gibt die Richtung des Feldes wider. (Bild: VH)

Aber zurück zu unseren elektrischen Dipolmomenten. Durch seinen Spin, also seinem Eigendrehimpuls, ist auch das Proton ein kleiner Kreisel und verhält sich nicht einfach so wie z.B. eine Kompassnadel im Magnetfeld. Legt man ein elektrisches Feld an, indem man das Proton zwischen zwei Platten mit entgegengesetzer elektrischer Ladung bringt, entseht eine Kraft, die den elektrischen Dipol entlang des elektrischen Feldes ausrichten möchte. Durch die Kreiseleigenschaft findet die Auslenkung aber senkrecht dazu statt: die Dipolachse und damit der Spin präzedieren um die Richtung des elektrischen Feldes. Die Geschwindigkeit dieser Präzession hängt von der Stärke des elektrischen Dipolmoments ab: je schneller die Präzession, desto größer das Dipolmoment. Und das ist genau das, was wir messen wollen.

Prinzip der EDM Messung (Bild: VH)

Für Neutronen lässt sich eine solche Messung auf relativ kleinem Raum durchführen. Protonen sind aber elektrisch geladen und werden daher im elektrischen Feld selbst abgelenkt. Daher fehlt noch ein Schritt  zum grundlegenden Messprinzip: statt einfacher Platten wird das elektrische Feld in einem Ring aufgebaut und das Proton in Bewegung versetzt. Dadurch fliegt das Proton auf einer Kreisbahn (durch die Ablenkung im Feld) und gleichzeitig präzediert der Spin.

Die Herausforderung besteht nun darin, dass einerseits das elektrische Dipolmoment so unvorstellbar klein ist und daher die Präzessionsbewegung auch extrem langsam ist, andererseits aber das Proton auch ein (sehr viel größeres) magnetisches Dipolmoment besitzt, das vergleichbare Effekte bewirkt. Aber wie sagt man so schön: wenn es einfach wäre, wäre es ja langweilig. Physiker wird man, um genau solche Herausforderungen anzunehmen.  Also: „Challenge accepted“.