Wie „dressiert“ man eigentlich Deuteronen? – Teil 3

Mein letzter Beitrag hatte mit Beschleunigerphysik und Polarisation ja herzlich wenig zu tun – zumindest auf den ersten Blick. Heute werde ich erklären, warum das auf den zweiten Blick doch so ist.Wir arbeiten mit Deuteronen, die in der horizontalen Ebene polarisiert sind, d.h. der Spin der Deuteronen liegt in der Ebene des Beschleunigerrings und die Spins zeigen idealerweise alle in eine Richtung. Während die Deuteronen sich im Beschleuniger (oder hier besser Speicherring) im Kreis bewegen, präzediert der Spin. Stellt man sich das Deuteronensemble als Kreisscheibe vor, auf dem ein Pfeil vom Mittelpunkt nach außen gemalt ist, dann heißt das, dass sich diese Scheibe pro Umlauf um ein Stück dreht. Den Teil eines Vollkreises, um den sich die Scheibe dreht, nennen wir Spintune: würde sich die Scheibe bei jedem Umlauf um 90 Grad drehen, wäre der Spintune ein Viertel, also 0.25.

Was hat das nun mit dem letzten Artikel zu tun? Sehen wir uns einmal das nächste Bild an:

Effekt der Spinrichtung auf die Messung (Bild: VH / Forschungszentrum Jülich)

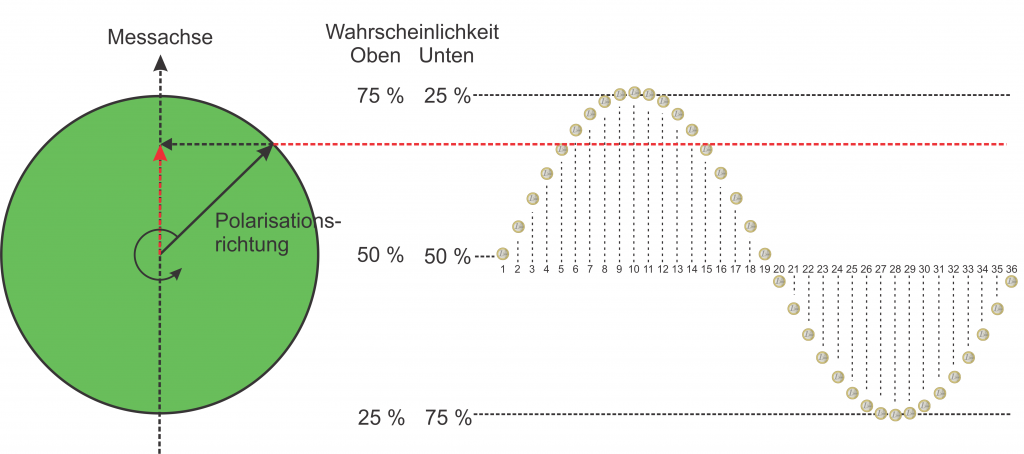
Das „Scheibenensemble“ ist links abgebildet und die Polarisationsrichtung als schwarzer Pfeil dargestellt. Messen können wir nur die Projektion  auf eine Messachse senkrecht zum Strahl. Dadurch wird die Präzession, also die Drehung in der Ebene, in genau die Kurve verwandelt, die ich beim letzten Mal für die Münzen verwendet hatte: Je nachdem wie groß der Anteil der Polarisation ist, die wir messen können, ändert sich die Wahrscheinlichkeit, ob ein gestreutes Teilchen nach oben oder nach unten fliegt.

Würde sich die Scheibe nun sehr langsam drehen und hätten wir die Zeit viele Messungen zu machen, könnten wir diese Kurve direkt messen (wie beim letzten Mal schon diskutiert). In der Realität ist die Situation aber so, dass die „Scheibe“ zwischen zwei Messungen mehrere komplette Umdrehungen absolviert.

Würden wir die Drehgeschwindigkeit der Scheibe kennen (also die Präzessionsfrequenz) könnten wir ausrechnen, in welche Richtung die Polarisation zeigt und so die Messpunkte der Kurve zuordnen. Tun wir aber nicht – oder genauer gesagt, nicht genau genug.

Das Deuteronenpaket umrundet COSY bei unserem Messungen etwa 750000 mal pro Sekunde. Wenn wir nun z.B. 2 Sekunden messen wollten und auch zum Schluss die Richtung innerhalb von 30 Grad noch stimmen soll, heißt das, dass ich die Präzession auf 0.00001 Grad pro COSY Runde kennen muss. Auf den Spintune umgerechnet ist das das 0.00000008ste einer Umdrehungen pro Umlauf. Das sind etwa drei bis vier Nullen zu viel (warum das so ist, darauf komme ich irgendwann noch einmal zurück).

Was also tun? Im Prinzip scannen wir ein Intervall in vielen kleinen Schritten um den erwarteten Wert der Präzessionsfrequenz herum und suchen nach der richtigen Frequenz. Da sich bei einer falschen Frequenz alle Polarisationseffekte wegmitteln, zeigt sich die richtige Frequenz so, dass bei ihr die rekonstruierte obige Kurve die größte Amplitude hat. Mathematisch ist das eine Fouriertransformation vom Zeitraum (Zeitpunkte der gemessenen Ereignisse) in den Frequenzraum (Präzessionsfrequenz), die sich auf verschiedene Arten realisieren lässt. Experimentell ließ sich das nur verwirklichen, indem wir alle Größen mit einer einzigen Uhr gemessen haben. So haben wir dann einerseits die Teilchenumläufe gezählt und andererseits genau mitgeschrieben, zu welchem Zeitpunkt ein Ereignis im Detektor registriert wurde – und zwar nicht relativ zu jeweils einem Ereignistrigger, sondern konsistent über den Zeitraum des kompletten Beschleunigerzyklusses hinweg. Durch die Normierung auf die Teilchenumläufe fielen dann auch alle Schwankungen in der Zeitmessung selbst wieder heraus. (Das Beitragsbild zeigt übrigens den EDDA Detektor, den wir für diese Messungen genutzt haben.)

Auf diese Art und Weise konnten wir den Spintune über einen kompletten Beschleunigerzyklus kontinuierlich messen (mittlerweile auch in Realzeit). Die Genauigkeit lag dabei bei dem 1 x 10^-8ten Teil einer Umdrehung pro Umlauf. Diese konnten wir noch weiter steigern, indem wir die aufeinander folgenden Messungen in einem Zyklus miteinander verbunden haben und uns nicht nur die Frequenz, sondern auch die horizontale Verschiebung der obigen Messkurve von Punkt zu Punkt (Phase) angeschaut haben. So kamen wir dann auf 1 x 10^-10.

Diese Messmethode ist die Grundvoraussetzung für alle weiteren Messungen und auch für die Möglichkeit an COSY ein erstes Experiment zur Bestimmung des Elektrischen Dipolmoments des Deuterons durchzuführen.  Über die nächsten erfolgreichen Schritte (Optimierung der „Spinkohärenzzeit“, d.h. wie lange die Deuteronen synchron präzedieren, und die aktive, dynamische Regelung des Spintunes) berichte ich dann in den kommenden Beiträgen – wahrscheinlich aber erst nach unseren nun anstehenden Experimentzeiten an COSY.